Characteristics
Tsunamis cause damage by two mechanisms: the smashing force of a wall of water travelling at high speed, and the destructive power of a large volume of water draining off the land and carrying all with it, even if the wave did not look large.
While everyday wind waves have a wavelength (from crest to crest) of about 100 metres (330 ft) and a height of roughly 2 metres (6.6 ft), a tsunami in the deep ocean has a wavelength of about 200 kilometres (120 mi). Such a wave travels at well over 800 kilometres per hour (500 mph), but owing to the enormous wavelength the wave oscillation at any given point takes 20 or 30 minutes to complete a cycle and has an amplitude of only about 1 metre (3.3 ft).[22] This makes tsunamis difficult to detect over deep water. Ships rarely notice their passage.
As the tsunami approaches the coast and the waters become shallow, wave shoaling compresses the wave and its velocity slows below 80 kilometres per hour (50 mph). Its wavelength diminishes to less than 20 kilometres (12 mi) and its amplitude grows enormously. Since the wave still has the same very long period, the tsunami may take minutes to reach full height. Except for the very largest tsunamis, the approaching wave does not break, but rather appears like a fast-moving tidal bore.[23] Open bays and coastlines adjacent to very deep water may shape the tsunami further into a step-like wave with a steep-breaking front.
When the tsunami's wave peak reaches the shore, the resulting temporary rise in sea level is termed run up. Run up is measured in metres above a reference sea level.[23] A large tsunami may feature multiple waves arriving over a period of hours, with significant time between the wave crests. The first wave to reach the shore may not have the highest run up.[24]
About 80% of tsunamis occur in the Pacific Ocean, but they are possible wherever there are large bodies of water, including lakes. They are caused by earthquakes, landslides, volcanic explosions glacier calvings, and bolides.
When the wave enters shallow water, it slows down and its amplitude (height) increases.
The wave further slows and amplifies as it hits land. Only the largest waves crest.
Drawback
If the first part of a tsunami to reach land is a trough—called a drawback—rather than a wave crest, the water along the shoreline recedes dramatically, exposing normally submerged areas.
A drawback occurs because the water propagates outwards with the trough of the wave at its front. Drawback begins before the wave arrives at an interval equal to half of the wave's period. Drawback can exceed hundreds of metres, and people unaware of the danger sometimes remain near the shore to satisfy their curiosity or to collect fish from the exposed seabed.
Shallow_water_wave.gif (466 × 70 pixels, file size: 1.29 MB, MIME type: image/gif, looped, 141 frames, 11s)
Scales of intensity and magnitude
As with earthquakes, several attempts have been made to set up scales of tsunami intensity or magnitude to allow comparison between different events.[25]
Intensity scales
The first scales used routinely to measure the intensity of tsunami were the Sieberg-Ambraseys scale, used in the Mediterranean Sea and the Imamura-Iida intensity scale, used in the Pacific Ocean. The latter scale was modified by Soloviev, who calculated the Tsunami intensity I according to the formula
where Hav is the average wave height along the nearest coast. This scale, known as the Soloviev-Imamura tsunami intensity scale, is used in the global tsunami catalogues compiled by the NGDC/NOAA and the Novosibirsk Tsunami Laboratory as the main parameter for the size of the tsunami.
Magnitude scales
The first scale that genuinely calculated a magnitude for a tsunami, rather than an intensity at a particular location was the ML scale proposed by Murty & Loomis based on the potential energy.[25] Difficulties in calculating the potential energy of the tsunami mean that this scale is rarely used. Abe introduced the tsunami magnitude scale Mt, calculated from,



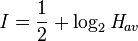






No comments:
Post a Comment